平方根概念、知识点及练习题
[10-20 18:09:40] 来源:http://www.67xuexi.com 初一数学 阅读:85470次
【性质与概念】
平方根的基础信息
一个正数如果有平方根,那么必定有两个,它们互为相反数。显然,如果我们知道了这两个平方根的一个,那么就可以及时的根据相反数的概念得到它的另一个平方根。
如果一个正数x的平方等于a,即x²=a,那么这个正数x叫做a的算术平方根。a的算术平方根记为![]() ,读作“根号a”,a叫做被开方数。
,读作“根号a”,a叫做被开方数。
规定:0的平方根是0。
负数在实数范围内不能开平方,只有在复数范围内,才可以开平方根。例如:-1的平方根为±1i,-9的平方根为±3i。
平方根包含了算术平方根,算术平方根是平方根中的一种。
任何复数都有平方根。
算术平方根为:√a=a(a为非负数)
被开方数是乘方运算里的幂。
求平方根可通过逆运算平方来求。
开平方:求一个非负数a的平方根的运算叫做开平方,其中a叫做被开方数。
若x的平方等于a,那么x就叫做a的平方根,即±√a=±x(a为非负数)
性质
与平方根的关系
正数的平方根有两个,它们为相反数,其中正数的平方根,就是这个数的算术平方根。
产生
根号(即算术平方根)的产生源于正方形的对角线长度“根号二”,这个 “根号二”的发现 一度引起了毕达哥拉斯学派的恐慌。因为按当时的权威解释(也就是毕达哥拉斯学派的学说),万物皆数(也就是说世界上所有的事物都可以用数来表示)。
对于这个无理数“根号二”,最终人们选取了用根号来表示。
举例
9的平方根为±3 ;9的算术平方根为3,正数的平方根都是前面加±,算术平方根全部都是非负数(0也在内,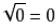 )
)
辨析
算术平方根和平方根是大家学习实数接触最多的概念,两者密不可分。可对于初学者来说是对“孪生杀手”,很容易在解题过程中产生错误。算术平方根和平方根到底有哪些区别与联系呢?
区别
1、定义不同:
⑴绝大部分地,如果一个正数x的平方等于a,即x2=a,那么这个正数x叫做a的算术平方根(arithmetic square root)。
⑵一般地,如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根(square root)。这就是说, 如果x2=a,那么x叫做a的平方根。
2、表示方法不同:
⑴a的算术平方根记为 读作“根号a”,a叫做被开方数(radicand)。
读作“根号a”,a叫做被开方数(radicand)。
⑵a的平方根记为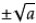 ,读作“正负根号a”,其中a叫做被开方数。
,读作“正负根号a”,其中a叫做被开方数。
3、个数不同:从形式上看,二者的符号主体相似,但是一个数的平方根要在其算术平方根的前面写上“±”。这也正好说明了一个正数和零的算术平方根有且只有一个,而一个正数却有两个互为相反数的平方根。零只有一个平方根。
联系
1、前提条件相同:算术平方根和平方根存在的前提条件都是“只有非负数才有算术平方根和平方根”。
2、存在包容关系:平方根包含了算术平方根,因为一个正数的算术平方根只是其两个平方根中的一个。
3、0的算术平方根和平方根相同,都是0。
【练习题】
1、正数a的平方根是( )

2、若m的平方根是±3,则m =______;若5x+4的平方根是±1,则x =______。
3、在−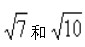 之间的整数是_____。
之间的整数是_____。
4、若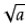 的算术平方根是3,则a =__。
的算术平方根是3,则a =__。
5、一个自然数的算术平方根是a,则下一个自然数的算术平方根是_____。
【参考答案】
1.B
2.9 由5x+4 = 1得x = −
3.−2,−1,0,1,2,3
4.81
5.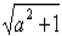
- 上一篇:立方根概念、知识点及练习题