平行线概念、知识点及练习题

　　【性质与概念】

　　平行线定义

　　在同一平面内，永不相交的两条直线叫做平行线。

　　平行线一定要在同一平面内定义，不适用于立体几何，比如异面直线，不相交，也不平行。

　　欧氏几何中平行线的性质

　　1.两条平行线被第三条直线所截，同位角相等。

　　2.两条平行线被第三条直线所截，内错角相等。

　　3.两条平行线被第三条直线所截，同旁内角互补。

　　以上性质可简单说成：

　　1.两条直线平行，同位角相等。

　　2.两条直线平行，内错角相等。

　　3.两条直线平行，同旁内角互补。

　　三角形中：

　　平行线分三角形对应边成比例。

　　平行线的判定

　　1.平行线的定义。(在同一平面内，不相交的两条直线叫做平行线。)

　　2.平行公理推论：平行于同一直线的两条直线互相平行。

　　3.在同一平面内，垂直于同一直线的两条直线互相平行。

　　4.同位角相等，两直线平行。

　　5.内错角相等，两直线平行。

　　6.同旁内角互补，两直线平行。

　　7.经过直线外一点，能且只能画一条直线与已知直线平行。

　　8.两条直线都平行于第三条直线，那么这两条直线平行。

　　平行公理

　　在同一平面内，过直线外一点，有且只有一条直线与这条直线互相平行。

　　在同一平面内，垂直于一条直线的两直线互相平行。

　　平行公理的推论：(平行线的传递性)，如果两条直线都和第三条直线平行，那么这两条直线也互相平行。

　　即平行于同一条直线的两条直线平行。简称：平行于同一条直线的两条直线互相平行。

　　平行线定义的拓展

　　在高等数学中的平行线的定义是相交于无限远的两条直线为平行线，因为理论上是没有绝对的平行的。

　　在欧氏几何中，在两条平行线中做一条直线AB，以直线AB为半径以逆时针方向做圆，然后以直线AB为半径以顺时针方向再做一个圆，从两个圆的交点做垂线CD垂直于直线AB，若CD与AB的角的角度是90度，则说明两条平行线不会相交。

　　但欧几里得不敢思考当两条平行线无限长时的情况.....

　　于是包括罗素、黎曼在内的科学家假设当两条平行线无限长时，他们会在无穷远处相交。(例如：在地球的球面上，就会发现，相互垂直于赤道的经线会相交于北极点和南极点。)后来，非欧几何和黎曼空间就诞生了，该成果给了爱因斯坦很大的启发。

　　平行线公理就是区分欧氏几何与非欧几何的一个重要区别。

　　【练习题】

　　1、下列命题：

　　①不相交的两条直线平行　　②梯形的两底互相平行

　　③同垂直于一条直线的两直线平行　　④同旁内角相等，两直线平行

　　其中真命题有( )

　　A.1个　　B.2个　　C.3个　　D.4个

　　2、下列命题：

　　①两个连续整数的乘积是偶数　　②带有负号的数是负数

　　③乘积是1的两个数互为倒数　　④绝对值相等的两个数互为相反数

　　其中假命题有( )

　　A.1个　　B.2个　　C.3个　　D.4个

　　3、如图，AB∥CD，AD∥BC，∠A=3∠B，求∠A、∠B、∠C、∠D的度数。

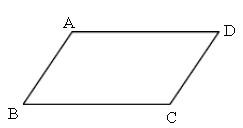
　　4、如图，B处在A处的南偏西45°方向，C处在B处的北偏东80°方向。

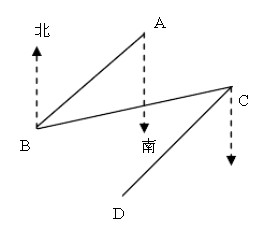
　　(1)求∠ABC。

　　(2)要使CD∥AB，D处应在C处的什么方向。

　　5、已知：如图，直线AB和CD相交于O，OE平分∠BOC， 且∠AOC=68°，则∠BOE=___

　　【参考答案】

　　1.B

　　2.B

　　3.135°　45°　135°　45°

　　4.(1)∠ABC=80°— 45°=35°

　　(2)要使CD∥AB，D处应在C处的南偏西45°方向

　　5.56°