高二数学 数列学习的7大方法

　　高二数学 数列学习的7大方法

　　1. 公式法

　　等差数列前n项和：

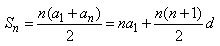
　　特别的，当前n项的个数为奇数时，，即前n项和为中间项乘以项数。

　　这个公式在很多时候可以简化运算。

　　等比数列前n项和：

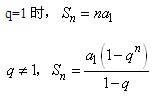　　，特别要注意对公比的讨论。

　　其他公式：

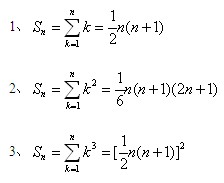
　　2. 错位相减法

　　这种方法是在推导等比数列的前n项和公式时所用的方法，这种方法主要用于求数列{an·bn}的前n项和，其中{a_n}、{b_n}分别是等差数列和等比数列。

　　３. 反序相加法求和

　　这是推导等差数列的前n项和公式时所用的方法，就是将一个数列倒过来排列(反序)，再把它与原数列相加，就可以得到n个。

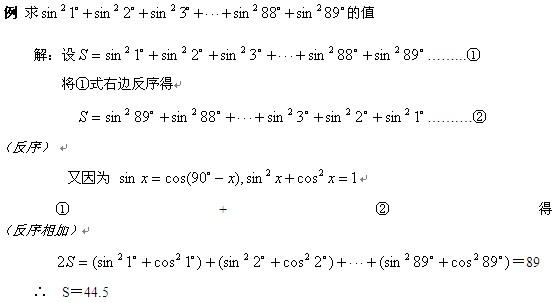
　　４. 分组法求和

　　有一类数列，既不是等差数列，也不是等比数列，若将这类数列适当拆开，可分为几个等差、等比或常见的数列，然后分别求和，再将其合并即可。

　　5. 裂项法求和

　　这是分解与组合思想在数列求和中的具体应用。裂项法的实质是将数列中的每项(通项)分解，然后重新组合，使之能消去一些项，最终达到求和的目的。通项分解(裂项)如：

　　6. 合并法求和

　　针对一些特殊的数列，将某些项合并在一起就具有某种特殊的性质，因此，在求数列的和时，可将这些项放在一起先求和，然后再求S_n。

　　7. 利用数列的通项求和

　　先根据数列的结构及特征进行分析，找出数列的通项及其特征，然后再利用数列的通项揭示的规律来求数列的前n项和，是一个重要的方法。

　　虽然数列是高二数学学习中的重点和难点，但是学习高二数学 数列还是有方法的，以上7种方法虽然各有特点，但总的原则是要善于改变原数列的形式结构，使其能进行消项处理，或者能使用等差数列，等比数列的求和公式以及其它已知的基本求和公式来解决，只要把握规律，就能使数列求和化难为易，迎刃而解。