平面向量概念、知识点及练习题

平面向量概念、知识点及练习题,标签：高二数学学习方法,高二学习计划,http://www.67xuexi.com

　　对于零向量和任意向量a，有：0+a=a+0=a。

　　向量的加法满足所有的加法运算定律，如：交换律、结合律。

　　减法

　　AB-AC=CB，这种计算法则叫做向量减法的三角形法则，简记为：共起点、连终点、方向指向被减向量。

　　-(-a)=a;a+(-a)=(-a)+a=0;a-b=a+(-b)。

　　数乘

　　实数λ与向量a的积是一个向量，这种运算叫做向量的数乘，记作λa。当λ>0时，λa的方向和a的方向相同，当λ<0时，λa的方向和a的方向相反，当λ = 0时，λa=0。

　　用坐标表示的情况下有：λAB=λ(x2-x1,y2-y1)=(λx2-λx1,λy2-λy1)

　　设λ、μ是实数，那么满足如下运算性质：

　　1.(λμ)a= λ(μa)

　　2.(λ + μ)a= λa+ μa

　　3.λ(a±b) = λa± λb

　　4.(-λ)a=-(λa) = λ(-a)

　　5.|λa|=|λ||a|

www.67xuexi.com

　　数量积

　　已知两个非零向量a、b，那么|a||b|cosθ(θ是a与b的夹角)叫做a与b的数量积或内积，记作a·b。零向量与任意向量的数量积为0。数量积a·b的几何意义是：a的长度|a|与b在a的方向上的投影|b|cos θ的乘积。

　　两个向量的数量积等于它们对应坐标的乘积的和。即：若a=(x1,y1),b=(x2,y2)，则a·b=x1·x2+y1·y2

　　数量积具有以下性质：

　　1.a·a=|a|2≥0

　　2.a·b=b·a

　　3.k(a·b)=(ka)b=a(kb)

　　4.a·(b+c)=a·b+a·c

　　5.a·b=0<=>a⊥b

　　6.a=kb<=>a//b

　　7.e1·e2=|e1||e2|cosθ

　　向量积

　　向量a与向量b的夹角：已知两个非零向量，过O点做向量OA=a，向量OB=b，则∠AOB=θ 叫做向量a与b的夹角，记作。已知两个非零向量a、b，那么a×b叫做a与b的向量积或外积。向量积几何意义是以a和b为边的平行四边形面积，即S=|a×b|。

　　若a、b不共线，a×b是一个向量，其模是|a×b|=|a||b|sin，a×b的方向为垂直于a和b，且a、b和a×b按次序构成右手系。若a、b共线，则a×b=0。

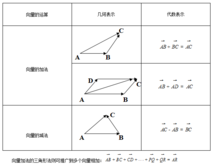
　　若a=(x1,y1,0),b=(x2,y2,0)，则有：

　　向量积具有如下性质：

　　1.a×a=0

　　2.a‖b<=>a×b=0

　　3.a×b=-b×a

　　4.(λa)×b=λ(a×b)=a×(λb)

　　5.(a+b)×c=a×c+b×c

　　混合积

　　给定空间三向量a、b、c，向量a、b的向量积a×b，再和向量c作数量积(a×b)·c，所得的数叫做三向量a、b、c的混合积，记作(a,b,c)或(abc)，即(abc)=(a,b,c)=(a×b)·c

　　混合积具有下列性质：

　　1.三个不共面向量a、b、c的混合积的绝对值等于以a、b、c为棱的平行六面体的体积V，并且当a、b、c构成右手系时混合积是正数;当a、b、c构成左手系时，混合积是负数，即(abc)=εV(当a、b、c构成右手系时ε=1;当a、b、c构成左手系时ε=-1)

　　2.上条性质的推论：三向量a、b、c共面的充要条件是(abc)=0

　　3.(abc) = (bca) = (cab) = - (bac) = - (cba) = - (acb)

　　四、平面向量基本定理

　　如果e1和e2是同一平面内的两个不共线的非零向量，那么对该平面内的任一向量a，有且只有一对实数λ、μ，使a= λe1+ μe2。

　　有关推论

　　1.三角形ABC内一点O，OA·OB=OB·OC=OC·OA，则点O是三角形的垂心。

　　2.若O是三角形ABC的外心,点M满足OA+OB+OC=OM，则M是三角形ABC的垂心。

　　3.若O和三角形ABC共面，且满足OA+OB+OC=0，则O是三角形ABC的重心。

　　4.三点共线：三点A,B,C共线推出OA=μOB+aOC(μ+a=1)

　　【练习题】

　　1. 设a=(2,-3),b=(x,2x),且3a·b=4,则x等于_____

　　2. 已知向量a+3b,a-4b分别与7a-5b,7a-2b垂直，且|a|≠0,|b|≠0，则a与b的夹角为____

　　【答案】

　　1.

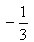
　　2.90°

上一页  [1] [2]